Action Priority¶
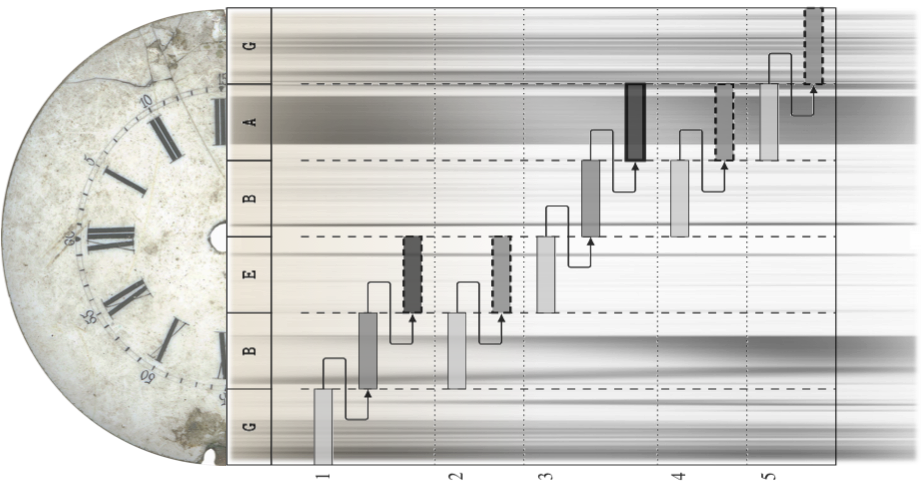
The Thickness of an instant¶
Each action performed by Antescofo occurs at some date and it may happen that several actions must be performed simultaneously “in the same logical instant”. This can be a problem. For example consider the fragment:
Group G1 { 1 $x := 0 }
Group G2 { 1 $x := 1 }
2 print $x
The two groups are launched in parallel and they schedule two
incompatible assignments to be performed at the same date, after the
expiration of a delay of one beat. The problem is to know what will be
printed when we print the value of $x? If we assume an
“ordinary” parallel execution, the outcome is not defined and the result
is either 0 or 1 but not deterministically: it varies from one
execution to the other.
The synchrony hypothesis used in the development of real-time embedded systems assumes that the actions that occur at the same date are performed in a specific and well defined order. Antescofo fulfills the synchrony hypothesis and the purpose of this section is to explain the execution order used to schedule actions at the same date. The rule is simple:
Achieving a deterministic execution was a major goal for Antescofo. So we describe in great details the ordering of simultaneous actions. However, the rest of this section can be skipped in a first reading.
Same Execution Date¶
A first remark is necessary: in this is section, when we speak about actions scheduled at the same date, we refer to two actions that must be performed at the same physical date, irrespective of their specification in the score.
Two actions that are specified at the same date in the score may well lead to two distinct execution dates. For example, in
NOTE C4 1
Group H1 @loose
{
1 $x := 0
; ...
}
Group H2 @tight
{
1 $x := 1
; ...
}
NOTE D3 1/2
the two assignments, which occur at the same date in the potential time of the score, may not happen at the same date during the performance because the groups H1 and H2 do not have the same synchronization strategy:
-
the assignment in
H2is performed when noteD3occurs, -
while the assignment in
H1is performed 1 beat after the occurrence ofC4(and the conversion from beat to physical time rely on the tempo estimated atC4).
These two instants are not necessarily the same: event D3
may occur earlier or later than the specification given in the
score. Thus, the value of $x depends of “external” events
(the musical events produced on stage) even if they coincide in the
score. These external events are not deterministic and do not depend on
Antescofo itself.
Conversely, two unrelated actions may, by chance, occur at the same date. For example:
NOTE E4 0.3
2 Group I1 { 3 $x := 0 }
3 Group I2 { 2 $x := 1 }
The two assignment to $x occur at the same date because
the sum of the delays occurring from the initial event (the occurrence
of the musical event which triggers the actions) are the same
(2+3 = 3+2). If they are really unrelated, their execution order
probably does not matter. But there are other cases when two actions are
clearly related in the score, are scheduled for the same date, and
indeed are executed at the same date. In this case, order matters and
the behavior of Antescofo must be easy to understand, deterministic
and relevant.
The Syntactic Ordering of Actions¶
The presentation in this paragraph and the next, does not apply fully to
the actions spanned by a whenever which will be
discussed below.
With the exception of whenever, the execution order
followed by Antescofo is simple: when two actions are scheduled at the
same date, the syntactic order \prec of appearance in the program is
used to determine which one is scheduled first. The syntactic order is
roughly the order of appearance in the linear score but takes into
account the nesting structure of compound actions.
More precisely, a vector of integers w(a), called the location of a, is associated with each action a. This vector locates uniquely the action a in the syntactic structure of the score. Two actions a and a' scheduled at the same date are performed following the lexicographic order of their location w(a) and w(a').
In the next example, we write vectors by listing their element separated by a dot: 1.2.3 is the vector with the three elements 1, 2 and 3. The location w(a) associated to an action a is build as follows:
-
Top-level actions (appearing before the first musical event or associated to a musical event) are identified by their rank i of appearance in the score: w(a) = i.
-
The ith action of a compound action
G, is located at w(G).i.
The lexicographic order is best explained in an example. The localization of each action is given on the left
1 $i := 0
2 Loop L1 1
{
2.1 print loop L1 iteration $i at $RNOW
2.2 $i := $i + 1
}
3 $j := 0
4 Loop L2 1
{
4.1 print loop L2 iteration $j at $RNOW
4.2 $j := $j + 1
}
and the actual trace is
loop L1 iteration 0 at 0.0
loop L2 iteration 0 at 0.0
loop L1 iteration 1 at 1.0
loop L2 iteration 1 at 1.0
loop L1 iteration 2 at 2.0
loop L2 iteration 2 at 2.0
loop L1 iteration 3 at 3.0
loop L2 iteration 3 at 3.0
loop L1 iteration 4 at 4.0
loop L2 iteration 4 at 4.0
Nota Bene:
-
The loop has a location which is distinct from the location of its body.
-
The syntactic order does not take into account the fact that an action may have several occurrences (this will be handled in the next paragraph).
This program exhibits several actions that occur at the same date:
-
The assignment to
$iand the start of the loop appears at the same date. The assignment is performed first because 1 \prec 2. -
For the same reason, the assignment to
$iis performed before the assignment of to$jand before the start of the loop . The start of loop is executed before the assignment to$j, etc. -
At time n, two prints occur together but the
printmessage inL1is issued before theprintmessage inL2because 2.1 \prec 4.1.
A Full Temporal Address with 3 Components¶
The syntactic order is based solely on the syntactic structure of the score and neglects the difference between an action and the (multiple) realizations of this action (called instances): for example, an action a in a loop is performed at each iteration. All of these instances are associated to the same location w(a). To compare these actions, that share the same location, we use their instance number.
This way, the temporal address of the execution of an action a has 3 components:
Temporal addresses are lexicographically ordered:
-
if two actions have the same date, then their locations (given order in the score) are used,
-
and if two actions have the same date and the same location, they are compared using their instance number (which is assigned at runtime and not by the composer).
In other words: two action instances that occur at the same date are ordered by their order of appearance in the score and if they are instances of the same action, they are ordered by seniority.
Relevance¶
The resulting order \ll is total: two different actions a and b are always comparable and a \ll b or b \ll a. Thus, this order entails a deterministic execution. The order \ll is not necessarily the order which is needed and there is no way to alter it in Antescofo. However, the corresponding scheduling seems relevant on several paradigmatic examples.
For instance, a classical problem is given by two nested loops:
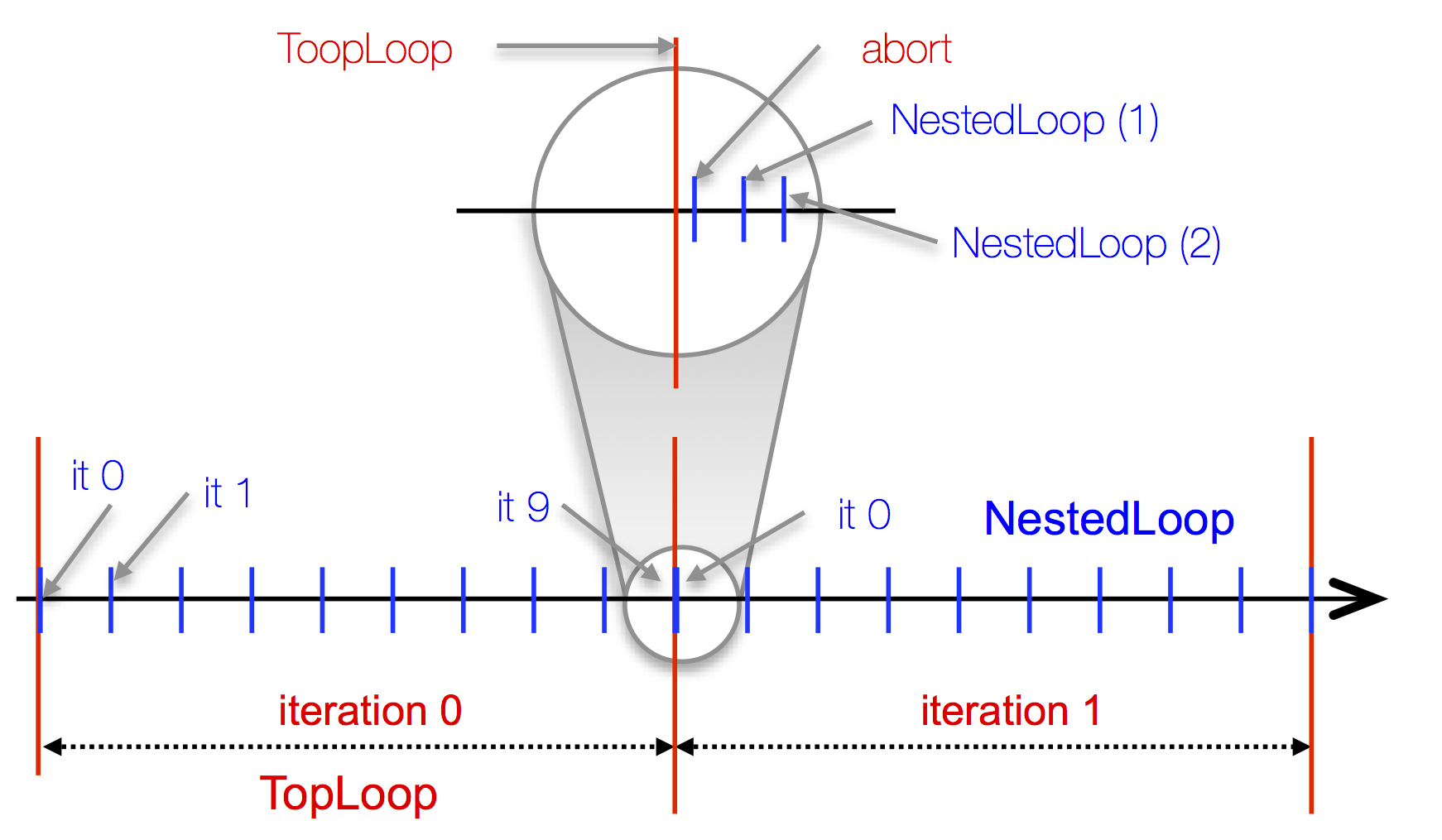
$lab := 0
loop TopLoop 1
{
abort $lab
$lab := {
Loop NestedLoop 0.1
{
$X := $X + 1
}
}
}
The loop TopLevel iterates a nested loop NestedLoop which assigns variable $X. The command
launched at iteration n of the TopLevel loop is
supposed to kill the NestedLoop spanned at the previous
iteration to avoid two assignments of $X at the same
date. The situation is pictured at the left of the program. Remark that
the expected behavior can be achieved without an explicit abort using
the @exclusive attribute.
Several actions share the same date:
-
The 10th assignment to
$Xin the ith instance ofNestedLoop. The temporal address of this assignment is (i, 2.2.1.1, 10 i). -
The first assignment to
$Xin the i+1th instance ofNestedLoop. The temporal address of this assignment is (i, 2.2.1.1, 10 i + 1). -
The
abortcommand issued by the i iteration ofTopLoop. The temporal address of this action is (i, 2.1, 10 i).
The final value of depends on the order of executions of these three
instances. For example, this result differs if the abort command is
issued after the two assignments or before. Because we have
$$
(i, 2.1, 10 i) \ll (i, 2.2.1.1, 10 i) \ll (i, 2.2.1.1, 10 i + 1)
$$
the command abort is issued first and cancel the 10th
assignment. So, when ::antescofo TopLoop is reiterated, there is only
one assignment that corresponds to the first iteration of the new
NestedLoop.
Scheduling of Whenevers¶
Whenevers span the execution of their body when activated by variable’s assignments. Thus, if an activation occurs at the same date as the firing of another action a, the order of the two depends of relative order between the assignment and a: the whenever body is activated as soon as the variable is assigned and if two whenevers are activated by the same variable, they are activated following their syntactic order. The resulting ordering cannot be solely deduced from the syntactic structure of the score. It is however deterministic.
Here are several examples. In the following fragment:
whenever W1 ($x > 0) { print A }
whenever W2 ($x > 2) { print B }
let $x := 3
A
B
the trace produced shows that W1 is activated before
W2. Indeed, the two whenevers are activated by the same
cause: the assignment to $x. In this case, the
whenever are activated following the syntactic order
explained above.
In this example
whenever W1 ($x) { print A }
whenever W2 ($y)
{
print B
let $x := 1
}
whenever W3 ($x) { print C }
let $y := 1
B
A
C
the activation order is W2 W1 W3 because the activation
of W1 and W3 are caused by the assignment
in the body of W2: so they cannot appear before the
activation of W2. Then, the activation of
W1 and W3 is done in this order,
following their syntactic order.
The next example shows that the order of activation is dynamic, i.e. it may depend of the values of the variables
whenever W1 ($x) { print A }
whenever W2 ($y) { print B }
if ($x > $y)
{
$x := $x + 1
$y := $y - 1
}
else
{
$y := $y + 1
$x := $x - 1
}
if $x > $y it will print
A
B
else it will print
B
A
In addition, do not forget that a whenever is activated at most once in a logical instant. So in the trace of the following fragment:
whenever W1 ($x || $y || $z)
{ print A }
whenever W2 ($x || $y)
{
print B
$z := true
}
$x := true
$y := true
will print
A
B
A and B appear only once.