Curve (continuous action)¶
Many computer music controls are by nature continuous. They are implemented by sampling in time the continuous variation of one or more parameters and performing some arbitrary action at each sampling point.
Curves in Antescofo allow users to define such continuous variations and the corresponding actions. They are two ways to specify these continuous variations:
-
In this section we rely breakpoint functions, another name for piecewise defined functions.
-
In the next section, we will use function defined by ordinary differential equations.
The programmer simply specify the continuous variations of the parameters and the corresponding actions (specified as an Antescofo group). The rest of the work is handled by the system which takes care of the computation the sampling points and the correct scheduling of the associate actions.
A breakpoint functions is defined by a sequence of interval. The value of the function is explicitly given on the borders of the interval and an interpolation method is specified for the points within this interval.
Curve based on breakpoint function may come in three flavors:
-
If the breakpoint function is defined by a linear interpolation on a single interval, then there is a simplified syntax which is very similar to the line construction in Max or PD. The user has few controls on such simplified curve. For instance, it cannot change the curve sampling rate.
-
The full curve syntax allow a fine control on the sampling process. It also make possible to specify vectorial curve. This additional expressivity comes with a price: the syntax is more complex than that of a simplified curve.
-
It is also possible to split appart the specification of breakpoint function and of the sampling process. in this case, the breakpoint function is defined elsewhere as a NIM data-structure and the curve construct can be seen as a NIM player. As time passes, the NIM is traversed and the corresponding action fired at the sampling point.
We introduce Curves starting with a simplified and familiar syntax of linear interpolation and move on to the complete syntax and showcase details of Curve construction.
Simplified Curve Syntax¶
The simplest continuous action to imagine is the linear interpolation of a scalar value between a starting and ending point with a duration, similar to line objects in Max or Pd. The time-step for interpolation in the simplified curve is 30 milli-seconds and hard-coded. This can be achieved using the simplified syntax as shown in
Curve level 0.0, 1.0 2.0 s
In this example, the action constructs a line starting at 0.0, going
to 1.0 in 2.0 seconds and sending the results to the receiver object
level. The initial point 0.0 is separated by a comma from the
destination point. The destination point consists of a destination value
(here 1.0) and the time to achieve it (2.0s in this case). At each
sampling point x, a message level x is sent to the
environment.
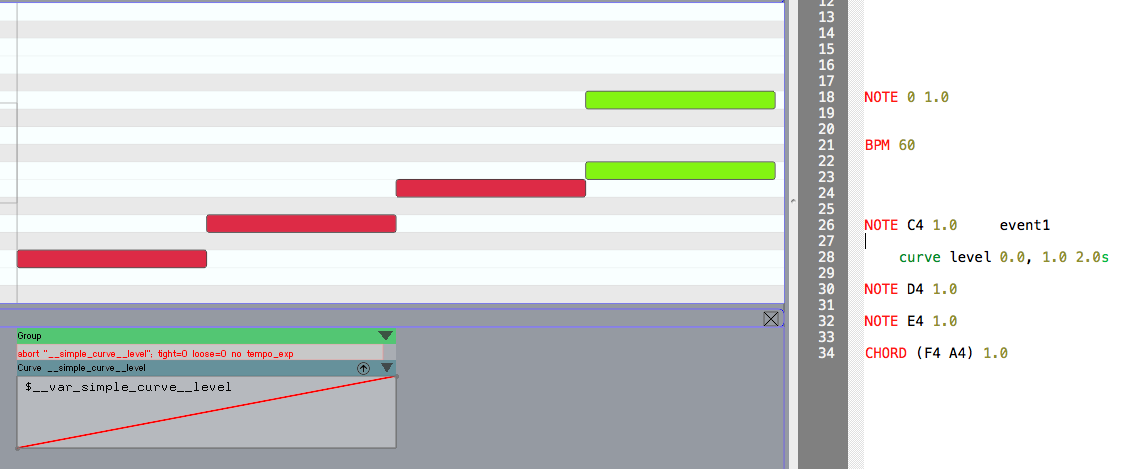
Chaining Simplified Curve¶
Another facility of Simplified Curves is their ability to be chained.
The score excerpt below shows the score where a second call to
curve level is added on the third note. This new call
does not have a starting point and only has a destination value:
Curve level 0.5 1.0
Both Curves also act on the same receiver level. This means that
during performance, the second curve will take on from whatever value of
the prior curve and arrives to its destination (here 0.5) at the given
time (here 1.0 beat).
This second curve takes precedence over the first, that is, it stops the first sampling process if needed and starts it sampling from the value reached by the first curve (which is not necessarily the final value if the second curve starts before the end of the first).
By calling simplified curves as above you can make sure that the first curve does not continue while the second is running. This is because of the way Simplified Curves are hard-coded. A new call on the same receiver/action will cancel the previous one before taking over.
Note that the second curve in the figure above cannot be visualised by Ascograph. This is because its starting point is a variable whose value is unknown and depends on where and when the prior curve arrives during performance.
The chaining may interleave the two forms almost arbitrarily: the first form defines a starting point and the second form starts from the last sampled value (so you must initiate the chaining with the first form).
The reason for the malleability of Simplified Curves is because they store their value as a variable. A new call on the same receiver aborts prior calls and takes the latest stored value as departing point if no initial point is given. You can program this yourself using the complete curve syntax.
The simplified curve is thus very similar to line object in Max or PD.
That said, it is important (and vital) that the first call to
Simplified Curve have an initial value. Otherwise, the departing point is
unknown and you risk receiving NaN values (not-anumber) until the
first destination point!
Performing Actions in a Simplified Curve¶
The action fired at the sampling point of a simplified curve is limited to two kind of actions:
-
updating the value of a variable with the sampled point,
-
or sending a message.
For the first case, you use a variable instead of a Max receiver in the curve construction:
curve $var starting_point , final_point duration
curve $var final_point duration
the sampled values will be assigned to the variable $var
by the curve. This variable can be used elswhere in the score. For
example, you can use a whenever construction to monitor the updates.
If the construct specify a message receiver, then at each sampling
point, the curve sends a message with a single argment: the sampled
value. Replacing the receiver with a bracketed @command
construct, it is possible to have more general messages and even to
compute the receiver of the message:
curve @command { receiver arg₀ arg₁ } starting_point , final_point duration
where receiver and the argᵢ are closed
expressions, will send the message:
@command(receiver) arg₀ arg₁ x
for each sampling point x of the curve (see the
@command keyword for computing the receiver of a message). The chained
version is similar:
curve @command { receiver arg₀ arg₁ } final_point duration
Summary of Simplified Curve¶
To summarize, starting a simplified curve is written:
curve max_receiver starting_point , final_point duration
curve $var starting_point , final_point duration
curve @command{ exp₀ exp₁ } starting_point , final_point duration
and chaining a simplified curve is written:
curve max_receiver final_point duration
curve $var final_point duration
curve @command{ exp₀ exp₁ } final_point duration
where cexp are closed expressions.
Full Curve Syntax¶
The simplified command hides several important properties of Curves from users and are there to simplify calls for simple linear and scalar interpolation. For example, the time-step for interpolation in the above curve is 30 milli-seconds and hard-coded. A complete curve allows for adjustment of such parameters, several kinds of multi-dimensional interpolations, complex actions, and more. From here we will detail the complete curve syntax.
A curve iterates a sequence of actions (specified with the @action attribute) on each sampling point (defined by the @grain attribute) of a piecewise function. The piecewise function is defined by multiple sub-functions, each sub-function applying to a certain interval defined by breakpoints. Between two breakpoints, the function is defined by an interpolation type, the delay between the breakpoint and the value of the general function at the breakpoints.
Piecewise functions defined this way are also called breakpoint functions or BPF. They are implemented in Antescofo as nim. Nim offers a powerful data structure to compute Piecewise functions and the curve construction acts as a nim player by sampling the nim in time.
In this section, we mainly discuss the curve construction that directly embeds the specification of the underlying BPF.
Scalar Curve¶
The example below shows a simple curve defined in two pieces. The
Curve has the name C and starts at a value
of 0. Two beats later, the curve reaches 2
and ends on 4 after 8 additional
beats. Between the breakpoints, the interpolation is linear, as
indicated by the string "linear" after the keyword
@type. Linear interpolation is the default behaviour of
a curve (hence it can be dismissed).
curve C
@action := { level $a },
@grain := 0.1
{
$a
{
{ 0 } @type "linear"
2 { 2 } @type "linear"
8 { 4 }
}
}
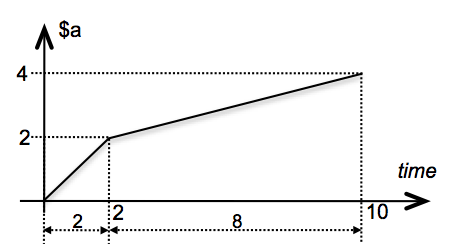
In the above example, variable $a, called the curve
parameter, ranges over the curve. Its value is updated at a time-rate
defined by attribute @grain which can be specified in
absolute time or in relative time. Each time $a is
updated, the @action sequence, which can refer to
$a, is triggered.
Vectorial Curve¶
It is easy to apply curves on multi-dimensional vectors as shown in the following example:
curve C
{
$x, $y, $z
{
{ 0, 1, -1 }
4 { 2, 1, 0 }
4 { -1, 2, 1 }
}
}
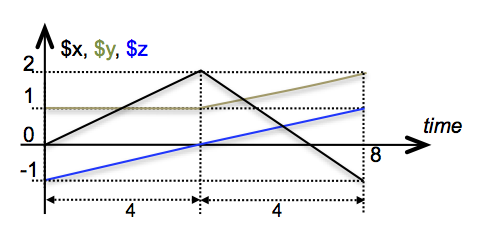
In the above example, all values in the three-dimensional vector share the same breakpoints and the same interpolation type. It is also possible to split the curve to multiple parameter clauses as below to allow different breakpoints between the curve elements:
curve C
{
$x
{
{ 0 }
2 { 0 }
0 { 1 }
3 { -1 }
}
$y
{
{ 1 }
3 { 2 }
}
}
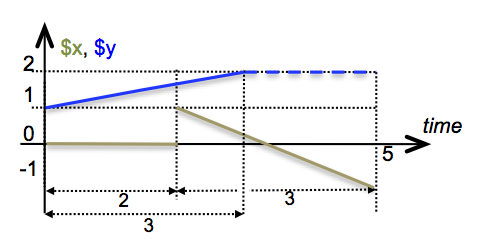
In the above example, curve parameters $x and
$y have different breakpoints. The breakpoint definition
on $x shows how to define a sudden change on a
step-function with a zero-delay value. Incidentally, note that the
result is not a continuous function on [0, 5]. The parameter is
defined by only one pair of breakpoints. The last breakpoint has its
time coordinate equal to 3, which ends the function before the end of
$x.
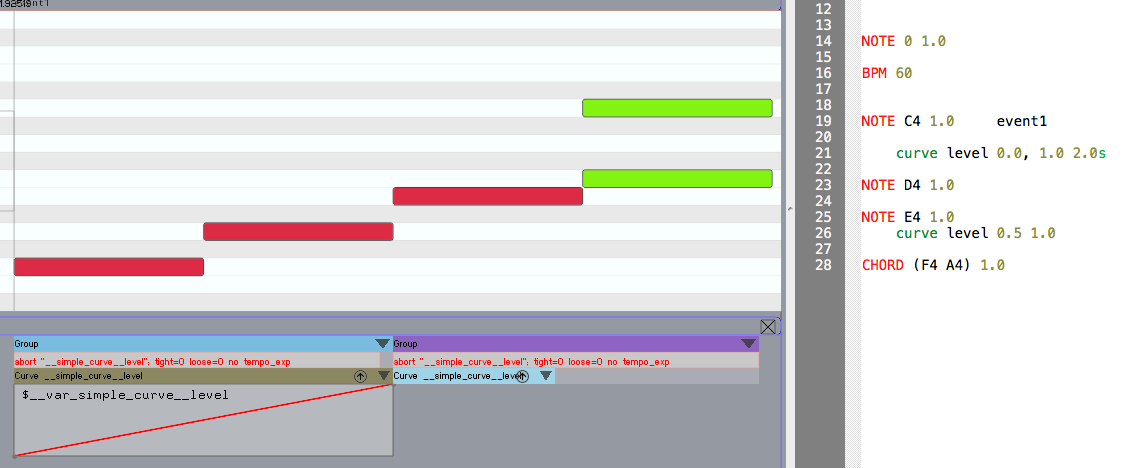
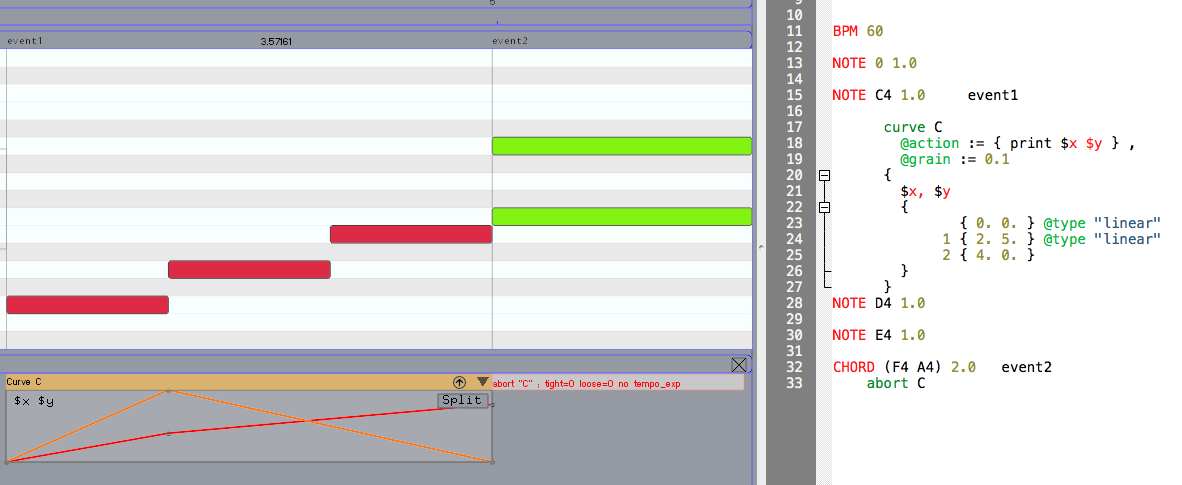
The figure [1] below shows a simple 2-dimensional vector curve on
Ascograph. Here, two variables $x and $y are used to sample the curve and are referenced in the action. They
share the same breakpoints but can be split within the same curve. The
curve is also aborted at event2 when the abort command
is called with the curve's name.
Editing Curve with Ascograph¶
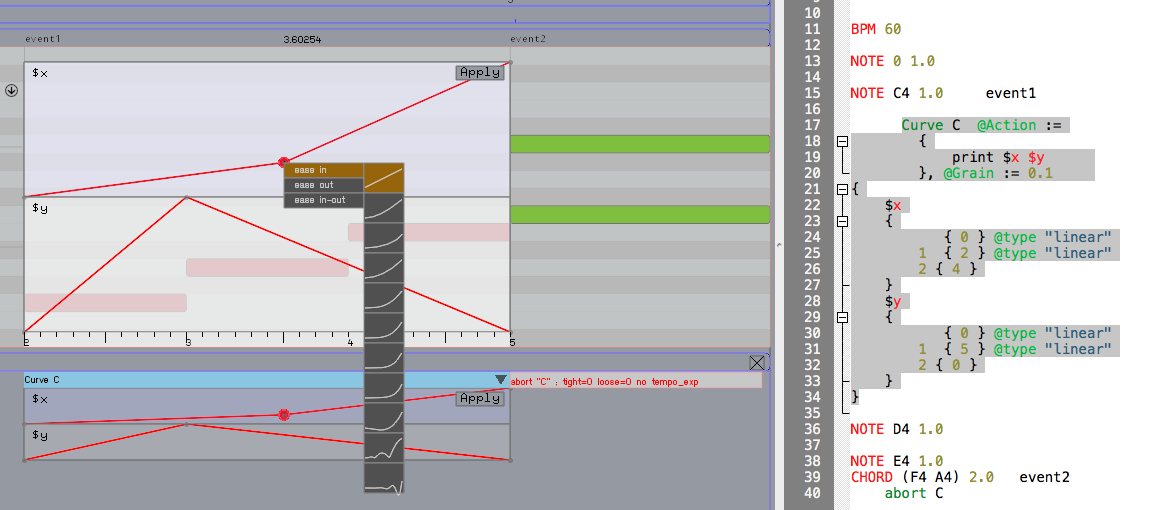
Using Ascograph, you can graphically interact with curves, as long as the curve parameters are constant. If this is the case, it is possible to move breakpoints vertically (changing their values) and horizontally (time position) by mouse, assigning new interpolation schemes graphically (control-click on breakpoint), splitting multi-dimensional curves and more.
For many of these operations on multi-dimensional curves, each coordinate should be represented separately. This can be done by pressing the button on the Curve box in which will automatically generate the corresponding text in the score. Each time you make graphical modifications on a curve in Ascograph, you need to press APPLY to regenerate the corresponding text.
The figure below shows the curve of the previous example [1] embedded on the event score, split and in the process of being modified by a user.
In the following sections we will get into details of Curve attributes: namely @action, timing @grain, and interpolation methods [@type]. But before that, we will describe the textual syntax. Knowing the textual syntax is important when defining curve whose parameters are defined by full expressions.
Textual Definition of a Full Curve¶
The body of the curve, the part between braces, takes various forms:
-
a sequence of explicit breakpoint specifying the value of the function at the breakpoints and the interpolation type between breakpoints (as exemplified previously);
-
sequence of symbolic breakpoints where the interval bteween breakpoints, the value at each breakpoints and the intrepolation type is not precisely given (only a general pace: increasing, decreasing, etc. is specified);
-
a nim which is value that represents a function (this value can be computed elsewhere);
-
a set of differential equations (this experimental feature is described in the next chapter).
Even if the specification of the body takes several forms, the principe of the curve is the same: the idea is to sample in time a function defined through a way or another.
Curve Attributes¶
NIM player¶
Breakpoints¶
Curve Interpolation Type¶
Actions Fired by a Curve¶
Each time a parameter is assigned, the action specified by the attribute @action is also fired. The value of the attribute is a sequence of actions. Usually, it is a simple message but arbitrary actions are allowed, for instance :
curve C
@action := {
print $y
2 action₁ $y
1 action₂ $y
}
{ ... }
At each sampling point, the value of $y is immediately
sent to the receiver print. Two beats later action₁ will be fired and one beat after that action₂
will be fired.
This sequence of actions is an implicit group and cannot have attributes, but a group can be nested for that end:
curve C
@action := {
Group @tempo := 120
{
print $y
2 action₁ $y
1 action₂ $y
}
}
{ ... }
If the @action attribute is absent, the curve simply assigns the parameters specified in its body. This can be useful in conjunction with other parts of the code if the parameters are refered in expressions or in other actions. In the next example, a curve is used to dynamically change the tempo of a loop
Curve
@grain := 5ms
{
$x { {60} 10 {120} }
}
Loop 1
@tempo := $x
{
print loop $NOW
}
until ($x >= 105)
0.0
0.954669
1.83255
2.64963
3.41704
4.14287
4.83321
5.49282
6.12547
6.73421
7.32156
Grain, Duration and Breakpoints Specifications¶
In the previous example, the time step (the sampling rate of the curve)
called grain size and specified with the @grain
attribute, is expressed in absolute time while breakpoints' durations
are expressed in relative time. However, durations and grains can be
freely expressed in absolute or relative time.
The grain size can be as small as needed to achieve perceptual continuity. However, in the MAX/PD environments, one cannot go below 1ms (the temporal resolution of the host1).
The grain specifies only a maximal duration between two sampling points. This freedom is used by Antescofo to ensure that the actions fired by the curve will be fired for each breakpoints boundaries.
Grain size and duration, as well as the values at breakpoints, can be closed expressions too. Grain size is evaluated at each sampling point, which makes it possible to change dynamically the time step.
The values of the breakpoint are evaluated once: when the curve is fired.
Curve Playing a NIM¶
A single value can be used as an argument of the curve parameter. In this case, the expression is expected to evaluate to a NIM, allowing the user to dynamically build breakpoints and their values as a result of computation. The syntax has already been described:
Curve ... { $x : e }
defines a curve where the breakpoints are taken from the value of the
expression e. This expression is evaluated when the curve
is triggered and must return a nim value. The NIM is used as a
specification of the breakpoints of the curve. Notice that, when a NIM
is “played” by a curve, the first breakpoint of the NIM coincides with
the start of the curve.
For example
$nim := NIM { ... }
; ...
Curve
@tempo := 30,
@grain := 0.1s,
@action := { print $x }
{ $x : $nim }
Any expression can be used which evaluates to a NIM. So, the following code plays a random NIM taken in a vector of 10 NIMs:
$nim1 := NIM { ...}
$nim2 := NIM { ...}
; ...
$nim10 := NIM { ...}
$tab := [ $nim1, $nim2, ..., $nim10 ]
; ...
Curve
@tempo := 30,
@grain := 0.1s,
@action := { print $x }
{ $x : $tab[@rand(11)] }
A typical situation is to play a NIM chosen from a repertoire of NIMs in
a specified time interval $dur. In this case, directly
playing the NIM with the curve is not appropriate, because the NIM will
be played with its natural length. Fortunately, processes like
NIMplayer make the desired behavior easy to code.
$Nim1 := NIM { 0. 0.,0.05 1 "quad",
0.1 0.2 "quad_out",
0.85 0. "cubic" }
$Nim2:= NIM { 0. 0.,0.05 1.,
0.9 1.,
0.05 0. }
@proc_def ::NIMplayer($NIM, $dur)
{
curve readNIM
@grain := 0.02s,
@action := { print ($NIM($x)) }
{
$x
{ { (@min_key($nim)) }
$dur { (@max_key($nim)) }
}
}
}
NOTE 69 4
::NIMplayer($Nim1, 4)
The playing of the NIM is controlled by a curve. The functions
@min_key and @max_key are used to get the definition interval of the
nim $nim.
Interpolation Methods¶
The specification of the interpolation between two breakpoints is given
by an optional string. The keyword @type is mandatory
only when a variable is used to specify the interpolation type. Using a
variable makes it possible to compute the interpolation type, e.g.
when a curve is embedded in a process and there is a need to
parameterize the interpolation type.
A linear interpolation is used by default. Antescofo offers a rich set of interpolation methods, mimicking the standard tweeners used in flash animation2. There are 10 different types:
-
linear, quad, cubic, quart, quint: which correspond to polynomial of degree respectively one to five;
-
expo: exponential, i.e. \alpha e^{\beta t + \delta} + \gamma
-
sine: sinusoidal interpolation \alpha \sin(\beta t + \delta) + \gamma
-
back: overshooting cubic easing (\alpha+1) t^3 - \alpha t^2
-
circ: circular interpolation \alpha \sqrt{(\beta t + \delta)} + \gamma
-
bounce: exponentially decaying parabolic bounce
-
elastic: exponentially decaying sine wave
With the exception of the linear type, all interpolations types come in three “flavors” traditionally called ease:
-
in (the default) which means that the derivative of the curve is increasing with the time (usually from zero to some value),
-
out when the derivative of the curve is decreasing (usually to zero),
-
and in_out when the derivative first increases (until the midpoint of the two breakpoints) and then decreases.
The corresponding interpolation keywords are listed below and illustrated in the next figures. Note that the interpolation can be different for each successive pair of breakpoints. These interpolation methods are also available for NIM (but NIM includes a richer set of interpolation types).
"back"
"back_in"
"back_in_out"
"back_out"
"bounce"
"bounce_in"
"bounce_in_out"
"bounce_out"
"circ"
"circ_in"
"circ_in_out"
"circ_out"
"cubic"
"cubic_in"
"cubic_in_out"
"cubic_out"
"elastic"
"elastic_in"
"elastic_in_out"
"elastic_out"
"exp"
"exp_in"
"exp_in_out"
"exp_out"
"quad"
"quad_in"
"quad_in_out"
"quad_out"
"quart"
"quart_in"
"quart_in_out"
"quart_out"
"quint"
"quint_in"
"quint_in_out"
"quint_out"
"sine"
"sine_in"
"sine_in_out"
"sine_out"
Programming an Interpolation Method.¶
If your preferred interpolation method is not included in the list above, it can be easily programmed. The idea is to apply a user defined function to the value returned by a simple linear interpolation, as follows:
@fun_def @f($x) { ... }
...
curve C
@action := { print (@f($x)) },
@grain := 0.1
{
$x
{ { 0 } @linear
1s { 1 }
}
}
The curve will interpolate function @f between
0 and 1 after it starts, over the course
of one second and with a sampling rate of 0.1 beats.
Examples of Interpolation Types¶
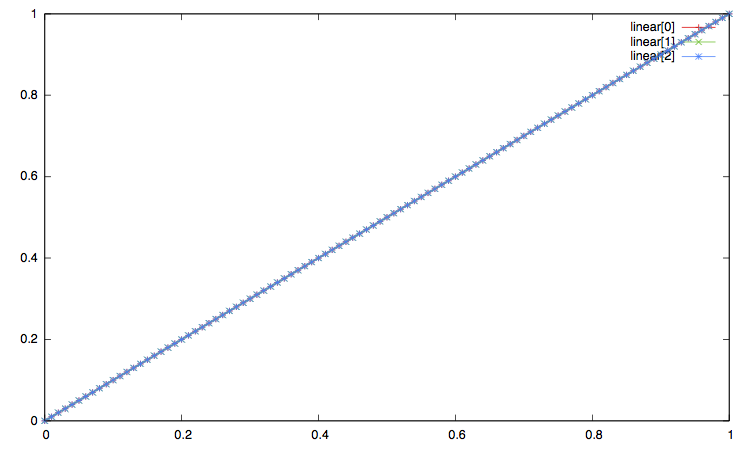
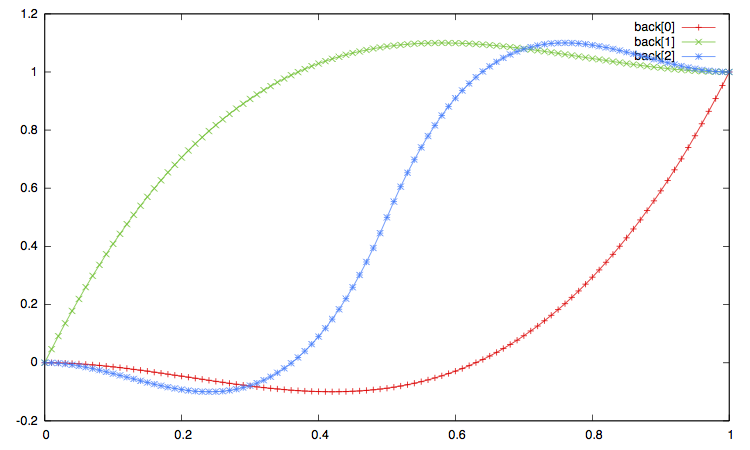
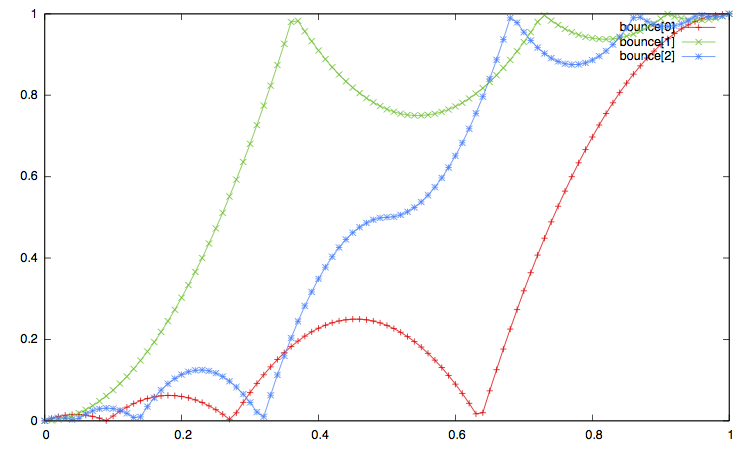
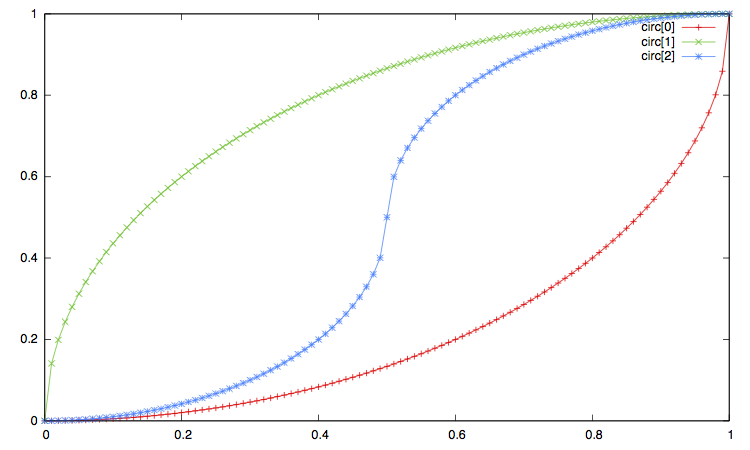
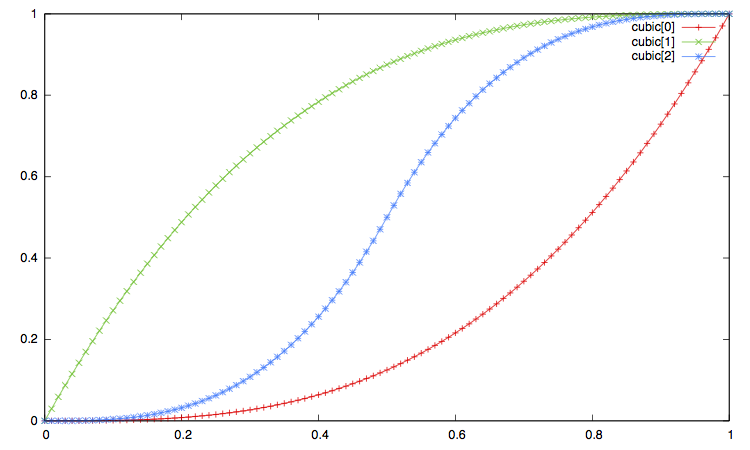
In the pictures below:
-
The label
xxx[0]corresponds to the ease in, that is to the type"xxx_in"or equivalently"xxx". -
The label
xxx[1]corresponds to the ease out, i.e. the interpolation type"xxx_out". -
And the label
xxx[2]corresponds to the ease in_out, i.e. interpolation method"xxx_in_out".
Open the imge on another window to enlarge the plot.
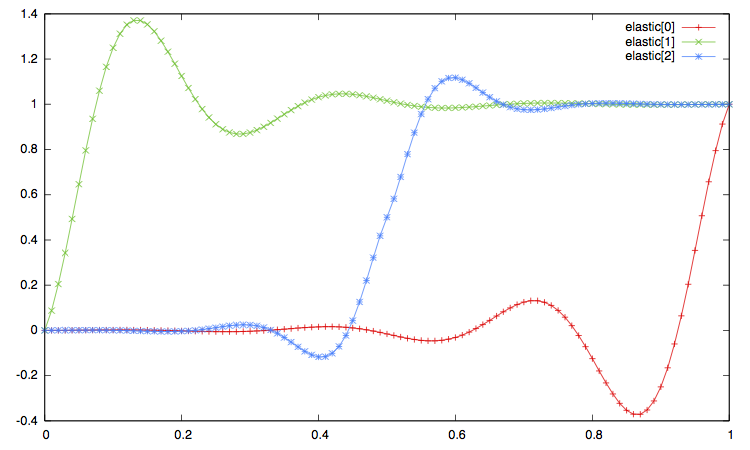
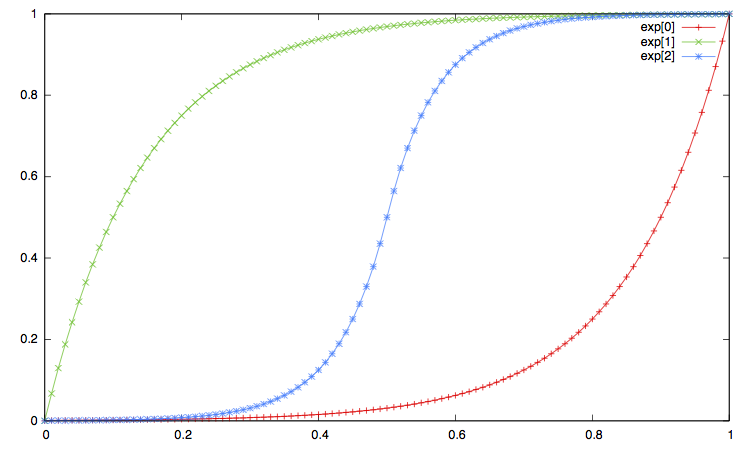
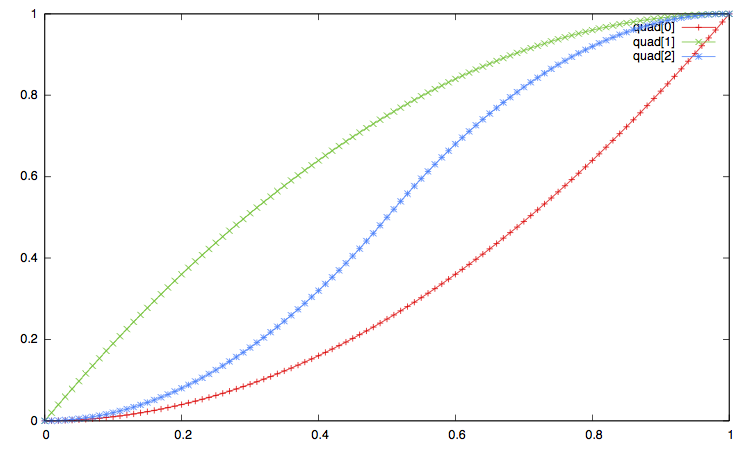
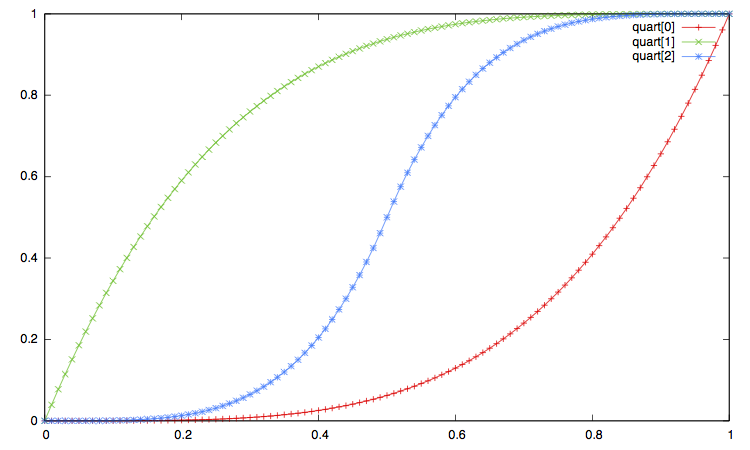
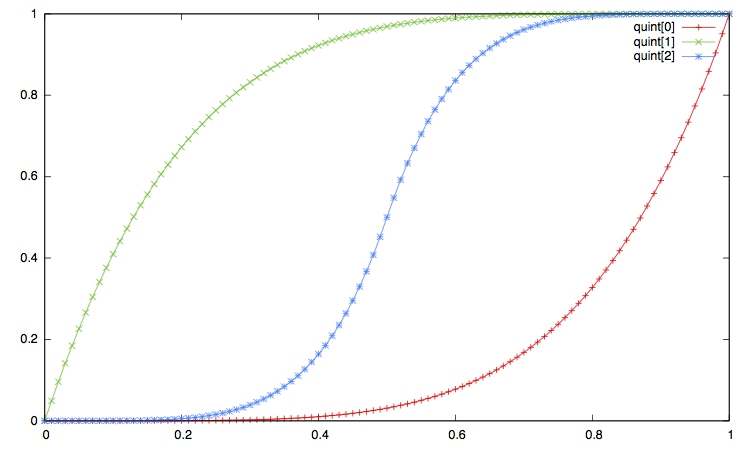
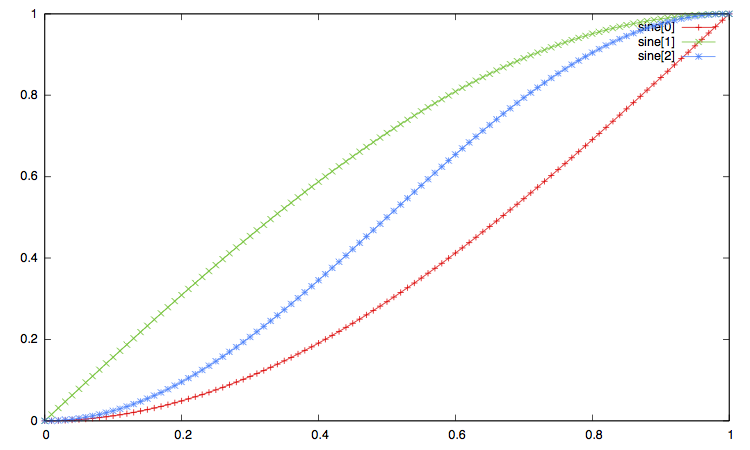
Curve Synchronization¶
Synchronization attributes apply to curve. To understand the effect of synchronization strategies on curve, it is usefull to understand the curve as a group whose actions are the curve's action iterated at each sampling point:
curve C
@grain := d
@action := { ... actionᵢ ... }
{ $x { {start} ... {end} } }
is really a shorthand for3:
Group G
{
$x := start
{ ... actionᵢ ... }
d $x := ...
{ ... actionᵢ ... }
d $x := ...
{ ... actionᵢ ... }
...
d $x := end
{ ... actionᵢ ... }
}
The synchronization attributes simply apply to this group.
-
Usually, the Max timer resolution is around 1ms and the temporal precision around 0.5ms. ↩
-
Inbetweening or tweening is the process of generating intermediate frames between two images to give the appearance that the first image evolves smoothly into the second image. The page Tweeners illustrates the standard tweens to control the successive positions of a point, illustrating the use of tweens to control the apparent speed and to achieve different qualities of movement. ↩
-
The equivalent group given here is only an approximation because the grain
dis dynamically computed and adjusted so that curve's action is executed for each breakpoint boundaries (breakpoint's duration are not necessary a multiple of the grain size). ↩