Group¶
The group construction gathers several actions logically
within one block that shares common properties of tempo, synchronization
and errors handling strategies in order to create polyphonic phrases.
The actions of a group are launched sequentially and the group organizes their precise temporal relationships: a group is a timeline and the actions of the group are actions scheduled on this timeline. Each group has a temporal scope which defines how time passes in the timeline. More generally, a temporal scope can be specified for all compound actions. Temporal scopes are implicitly defined through attributes of compound actions: @tempo and synchronization attributes. This notion will be developped in the next chapter Management of Time. In this chapter, we focus on the syntax and the hierarchical structure of compound actions.
The general syntax of a group is defined by the following diagram:
The specification of the label, Attributes and end clause are
optional. The label is a simple identifier that acts as a label for
the group.
There is a short notation for a group without optional parameters and attributes: its actions are simply be written between braces. For example:
action₁
{ 0.5 action₂ }
action₃
is equivalent to
action₁
Group {
0.5 action₂
}
action₃
Implicit Groups¶
Some groups are implicit. For example, the actions following an event are
members of an implicit group named top_gfwd_xxx where xxx is a
unique number in the score 1. And all child actions of a compound
action take place in a implicit group, often called the body of this
compound action (e.g., the body of a loop, the body of a process,
etc.).
By default, the implicit top-level groups are created with the @loose
synchronization strategy. This behavior can be changed in favor of the
@tight synchronization strategy, using the command top_level_groups_are_tight at the begining of the score.
Action Sequence¶
The actions of a group are arranged in a sequence. Two consecutive actions in this sequence are launched together, in parallel. For instance
let $x := 0
print $x
will be launched in the same instant. Nevertheless, actions that
occur in the same instant are ordered: this is the synchrony
hypothesis. So, in the previous example, a 0 will be printed.
The temporal scope of a group is used to interpret the relative delays that appears optionally in front of an action. For example:
Group G @tempo := 120
{
1 action₁
2 action₂
}
With the launch of group G, the delay of the first action
is evaluated into 1, and then nothing happens until 1 beat at tempo
120 is elapsed. At this moment action₁ is launched and
the delay preceeding action₂ is evaluated. Etc.
The quantity of physical time corresponding to a relative delay is specified by the tempo of the group. The way of counting this quantity depends of the synchronization strategy of the group.
The sequencing of actions in a group can be modified using
continuation operators. The ==> operator is used to
launch an action after the end of the preceding one and +=> is used to launches at the end of the previous one including its
children. The end of a group is the launch of the last action in its
action sequence (if this action has a delay, the group ends with the
start of this delay). For example
let $start := $RNOW
Group G
{
1 action₁
2 action₂
Group GG
{
1 action₃
1 action₄
}
}
==> print OK ($RNOW - $start)
will print OK 3 ($RNOW gives the relative time) because
G ends at soon as GG is started and
GG is started with action₂. But, if the
continuation operator ==> is changed for +=>:
let $start := $RNOW
Group G
{
1 action₁
2 action₂
Group GG
{
1 action₃
1 action₄
}
}
+=> print OK ($RNOW - $start)
then OK 5 will be printed because the +=> operator will
execute the print message at the end of all actions spanned directly
or indirectly by G.
These features will be discussed more in depth in chapters continuation and temporal scope.
The Nested Structure of Groups¶
Groups, and more generally compound actions, can be nested arbitrarily. We illustrate below the nesting of groups specified by
Group G
{
action₀
1 action₁
Group G1
{
action₂
1 action₃
action₄
}
2 Group G2
{
3 action₅
action₆
}
action₇
Group G3
{
action₈
Group G31
{
2 action₉
action₁₀
}
action₁₁
}
}
as a tree making explicit the father/child relationships
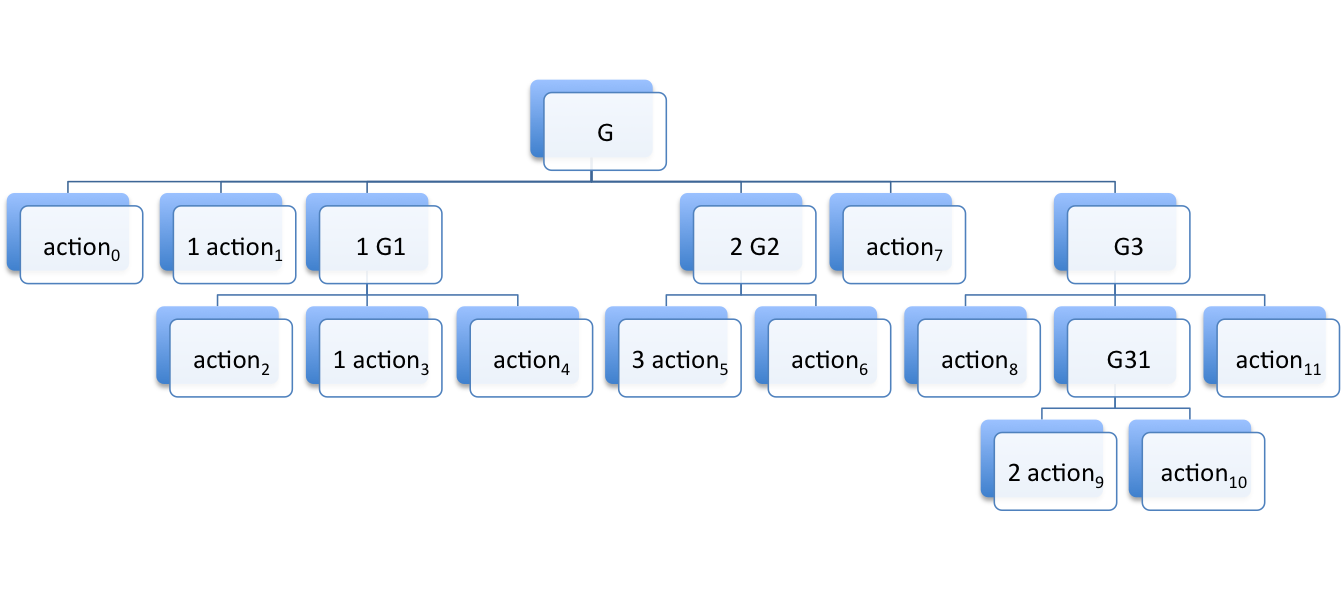
and as a timeline showing the temporal organization
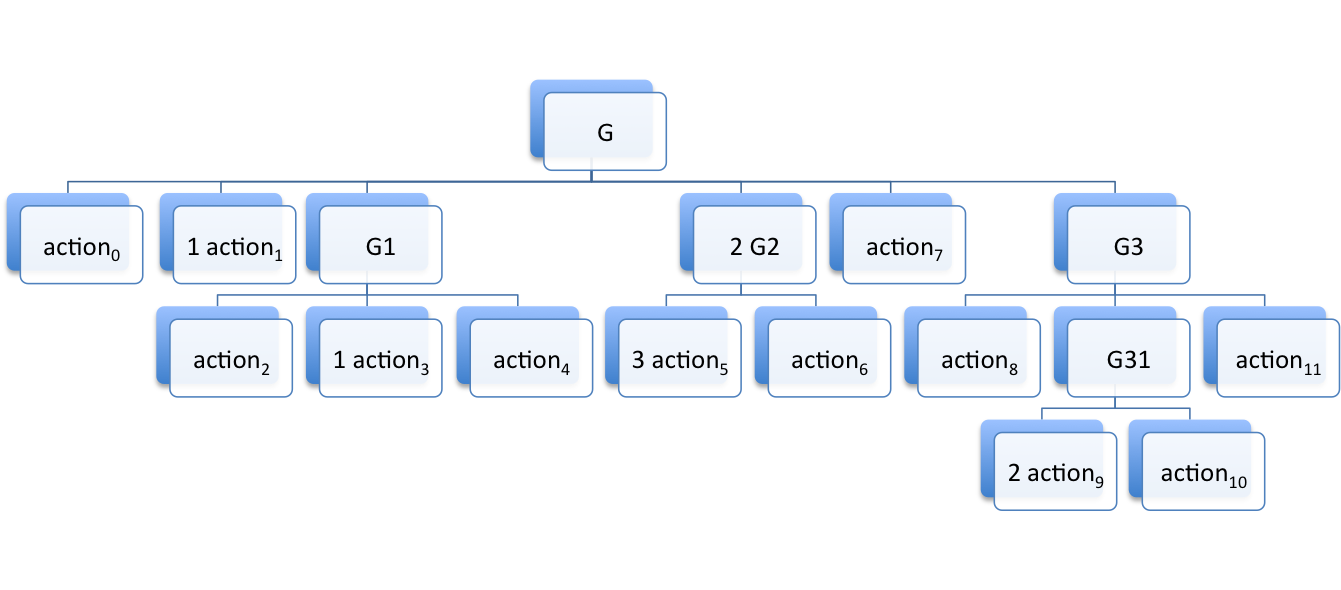
In this last diagram, the width of an action actionᵢ
(abbreviated aᵢ) is not relevant. A group is pictured as a rectangle
containing its childs but this is merely a graphical convention: a group
ends with the start of its last action.
Instances of a Group¶
A group is related to either an event or another action. When the event occurs or the action is triggered, the group waits for the expiration of its delay before sequentially launching the actions that comprise it. We say that an instance of the group is created and launched. The instance is considered alive while there is an action of the group waiting to be launched. In other words, an instance expires when the last action of the corresponding group is performed. It is possible to refer to the instance of a group through a special kind of values called Exec.
We make a distinction between the group and its instances because
several instances of the same group can exist and can even be alive
simultaneously. Such instances are created by loop,
forall, etc. These constructions are described in the
rest of this chapter.
Local variables¶
Variables local to a sequence of actions can be declared using the @local keyword. A @local declaration is not an action, and can appear anywhere in the sequence. The introduced variable is:
-
local to each instance of the action sequence (two instances do not share the variable);
-
its scope (where the variable's name is recognized) is the whole sequence where it is defined and all enclosed actions;
-
and its lifetime (when the variable can be read and written) is the lifetime of the sequence and its children. The variable cease to exist once the last nested action has expired.
Notice that a local variable can be safely accessed by a child action, even if the group where it has been defined has expired.
See section Variables for further information.
Aborting a Group¶
There are several ways to provoque the premature end of a group, or more generally, of any compound action:
Note that when the name of a group is used in an abort action, all alive instances of this group are killed. It is possible to kill a specific instance using the exec that refers to this instance.
The two last mechanisms are called end clauses.
The until and the while Clause¶
The specification of a group may include an optional
until clause that is checked before the triggering of an
action of the group:
$x := false
Group G {
1 $x := true
1 print DONE
} until ($x)
The word DONE will never be printed because the group is aborted when
$x becomes true. More exactly the expression
$x is checked each time a action must be launched. And if
true, the group is terminated instead of proceeding with the action. So,
with the following program:
{
$x := false
1 $x := true
1 $x := false
}
Group G {
3 print DONE
} until ($x)
the word DONE will be printed even if the $x variable
has been set to true. As a matter of fact, at date 3
beats, the variable is false again (notice that in
{ ... } Group G { .... } there are two groups that are
spanned in parallel).
There is another way to represent the until keyword:
using the contrary while statement. Thus,
group ... { ... } until (exp)
is equivalent to
group ... { ... } while (! exp)
The during Clause¶
A during clause specifies temporal validity, i.e.
the time a group is active. When this time is exhausted, the group is
aborted. This time can be specified
-
in beats (relative time):
[d] -
in (milli-)seconds (absolute time):
[d s]or[d ms ] -
or in number of logical instants:
[d #].
For instance:
Group G {
1 $x := true
1 print DONE
} during [1.5]
will launch the assignment 1 beat after the launching of but the message
print is never sent because is aborted 1.5 beats after
its start.
The notation of a duration follows the notation used for the access to the history of a variable. So
Group G {
; ...
} during [1.5 s]
will execute the actions specified by the group, up to 1.5 seconds after its start. And
Group G {
; ...
} during [1 #]
will execute the group only once. For example
Group GG
{
print GG 1
1 print GG 2
1 print GG 3
1 print GG 4
1 print GG 5
1 print GG 6
1 print GG 7
} during [4#]
will print:
GG 1
GG 2
GG 3
GG 4
because 4 logical instants after its activation, the group GG is aborted.
This last logical duration may seems useless for a group, but is very convenient to specify the number of iterations of a loop or the maximal number of triggering of a whenever.
The @abort clause¶
Every compound action may have an abort handler specified through the @abort attribute. The abort handler is a sequence of actions performed when the compound action is terminated via an abort. It is not performed when the group reaches is natural end or if it is terminated via an end clause.
The scope of the handler is the scope introduced by the compound actions (if any): local variables introduced by the compound action are accessible in the handler.
For example
Group G @abort { print "DONE" }
{
print G 0
1 print G 1
1 print G 2
1 print G 3
}
1.8 abort G
will print:
G 0
G 1
DONE
A typical example of an abort handler is illustrated in section abort handler: they are used to stop a curve arbitrarily with a “fade” leading the parameter to reach a final value irrespectively of its value when the abort occurs.
The @exclusive Clause¶
The last figures of the previous section
show that multiple instances of the same group spanned by a compound
action may overlap in time. Sometimes it is necessary to avoid this
behavior: this can be achieved using an @exclusive
attribute on the compound action.
The effect of @exclusive is to abort any previous
instances of the group (if they are still active) when a new instance is
triggered. The termination includes the eventual children of the
previous instances. Abort handlers are activated if there are any. The
new instance is triggered after the termination process.
Synchronization Attributes¶
Synchronization strategies like @loose and
@tight
group ... @loose ... { ... }
group ... @tight ... { ... }
and error strategies like @local and @global
group ... @global ... { ... }
group ... @local ... { ... }
can be specified for a group and also for every compound
action using the corresponding attributes. If they are not explicitly
defined, the attributes of an action are inherited from the
enclosing action. Thus, using compound actions, the composer can easily
create nested hierarchies (groups inside groups) sharing homogeneous
behaviors.
Synchronization strategies are described in chapter Synchronization Strategies.
Local Tempo¶
A local tempo can be defined for a group using the attribute @tempo:
group G @tempo := exp ... { ... }
exp is an arbitrary expression that defines the passing of time for
the delay of the actions of that are expressed in relative time in the
group, see chapter Management of Time.
With a local tempo, you can create, for example, an accelerando. In the next example, we use a variable to specify a local tempo and we control this variable with a curve (see Curve). That way, we can write a group where all durations are equal. It’s the variation of the local tempo variable that creates the accelerando.
curve tempVariation @grain := 0.05s
{ $localtemp
{ { 60 } 1 { 120 } }
}
group G @tempo := $localtemp
{
action1
1/4 action2
1/4 action3
1/4 action4
1/4 action5
1/4 action6
1/4 action7
1/4 action8
}
-
This name may appears in some error messages or in the listing generated by the command antescofo::printfwd following the verborsity level. ↩