@linearize(nim, tol:numeric)
build a new nim that approximates the argument. The new nim uses only linear interpolation and homogeneous breakpoints. An adaptive sampling step achieves an approximation within tol (i.e. for any point in the domain, the images of the nim argument and the image of the resulting nim are withing tol) .

The result is a linear homogeneous nim.

The application of the @linearize function can be time consuming and care must be taken to not perturb the real-time computations, e.g., by precomputing the linearization: see [eval_when_load] clause and function @loadvalue.

See also @align_breakpoints, @sample and the nim simplification functions: @simplify_radial_distance_t, @simplify_radial_distance_v, @simplify_lang_v, @filter_median_t, @filter_min_t, @filter_max_t, @window_filter_t

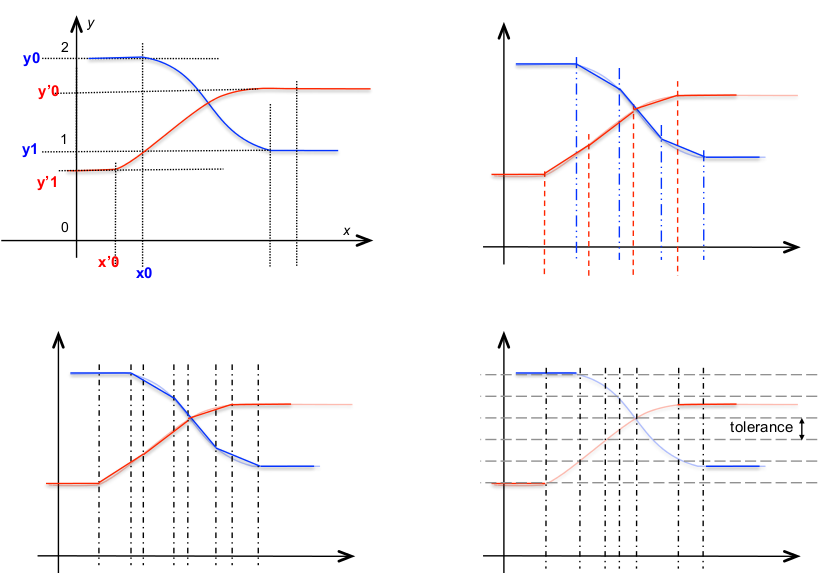
In the figure below, the diagram at the top left shows a vectorial nim with two components:

  • the effect of @sample is pictured at top right,

  • the effect of @align_breakpoints is sketched at bottom left,

  • and the effect of @linearize is illustrated at bottom right.

the effect of @sample, @align_breakpoints and @linearize on a nim